Manipulação de Dados com Pandas

Author

Vinícius Oviedo

Métodos estatísticos

Nesta aula, vamos trabalhar com medidas de estatística descritiva em Pandas. Aqui, vamos utilizar um conjunto de dados disponível na biblioteca seaborn, uma biblioteca de visualização de dados. O conjunto de dados trata de contas e gorgetas em um restaurante fictício. O conteúdo a ser discutido é:

Método describe()
Obtenção de valores máximo e mínimo, além da amplitdue dos dados
Medidas de tendência central: média, mediana e moda
Medidas de dispersão: desvio padrão, variância, coeficiente de variação
Medidas de posição: quartis, percentis, mediana
Outliers via método IQR
Correlação entre variáveis.

Primeiramente, vamos carregar o conjunto de dados tips, além das bibliotecas necessárias:

import pandas as pd
import seaborn as sns

tips = sns.load_dataset('tips')
tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

1. Estatísticas descritivas

As estatísticas descritivas podem ser obtidas pelo método .describe()

# Vamos mostrar a tabela transposta (T) fins de visualização (linhas viram colunas):
tips.describe().T

	count	mean	std	min	25%	50%	75%	max
total_bill	244.0	19.785943	8.902412	3.07	13.3475	17.795	24.1275	50.81
tip	244.0	2.998279	1.383638	1.00	2.0000	2.900	3.5625	10.00
size	244.0	2.569672	0.951100	1.00	2.0000	2.000	3.0000	6.00

Nesse dataframe de saída temos:

Coluna	Descrição
COUNT	Contagem
MEAN	Média
STD	Desvio padrão
MIN	Valor mínimo
25%	Primeiro quartil (`Q1`, 25% dos dados)
50%	Segundo quartil ou mediana (`Q2`, 50% dos dados)
75%	Terceiro quartil (`Q3`, 75% dos dados)
MAX	Valor máximo

Dica:

Caso queiramos menter dados categóricos também, podemos incluir a opção include='all'.

2. Mínimo, máximo e amplitude

Com essas medidas, podemos responder algumas perguntas.

Qual foi a gorjeta mínima?

tips['tip'].min()

1.0

Qual foi a maior conta (máximo total_bill)?

tips['total_bill'].max()

50.81

Logo a amplitude dos dados (para a coluna tip) pode ser obtida por:

\[ A = Max - Min \]

amplitude_gorjetas = tips['tip'].max() - tips['tip'].min()
amplitude_gorjetas

9.0

3. Medidas de tendência central

Média

tips['tip'].mean()

2.99827868852459

Mediana

tips['total_bill'].mode()

0    13.42
Name: total_bill, dtype: float64

Moda

tips['day'].mode()

0    Sat
Name: day, dtype: category
Categories (4, object): ['Thur', 'Fri', 'Sat', 'Sun']

Conferindo:

tips['day'].value_counts()

day
Sat     87
Sun     76
Thur    62
Fri     19
Name: count, dtype: int64

4. Medidas de dispersão:

Desvio Padrão

# Amostra (padrão, ddof=1):
print(tips['tip'].std())

# População:
print(tips['tip'].std(ddof=0))

1.3836381890011822
1.3807999538298954

Variância

# Amostra (padrão, ddof=1):
print(tips['tip'].var())

# População:
print(tips['tip'].var(ddof=0))

1.914454638062471
1.9066085124966412

Coeficiente de variação (CV)

# Amostra:
cv_gorjeta = tips['tip'].std(ddof=1) / tips['tip'].mean() *100
cv_gorjeta = round(cv_gorjeta, 2)
print(f' CV para tip: {cv_gorjeta}')

 CV para tip: 46.15

5. Medidas de posição:

Quartis

Q1 = tips['tip'].quantile(0.25)
Q2 = tips['tip'].quantile(0.5)
Q3 = tips['tip'].quantile(0.75)

print(f'Q1 (25%): {Q1}')
print(f'Q2 (50%): {Q2}')
print(f'Q3 (75%): {Q3}')

Q1 (25%): 2.0
Q2 (50%): 2.9
Q3 (75%): 3.5625

Isso diz muito sobre a distribuição dos dados e pode ser visualizado por um boxplot:

sns.boxplot(data=tips, x='tip', width=0.2, palette='viridis_r')

Percentis

# Percentil 90°:
tips['tip'].quantile(0.9)

5.0

6. Outliers via método IQR

A partir do conhecimento dos quartis e da distância inter-quartil (IQR), dada pela diferença Q3-Q1, podemos encontrar outliers (valores discrepantes):

\[ Outliers \ Inferiores = Q_1 - 1.5 IQR \]

\[ Outliers \ Superiores = Q_3 + 1.5 IQR \]

Assim, vamos encontrar outliers para a coluna total_bill.

IQR = tips['total_bill'].quantile(0.75) - tips['total_bill'].quantile(0.25)
outliers_inf = tips['total_bill'].quantile(0.25) - 1.5*IQR
outliers_sup = tips['total_bill'].quantile(0.75) + 1.5*IQR

print(f'Outliers inferiores: {outliers_inf}')
print(f'Outliers superiores: {outliers_sup}')

Outliers inferiores: -2.8224999999999945
Outliers superiores: 40.29749999999999

Do ponto de vista prático, gorjeta negativa não faz nenhum sentido. Logo, podemos concluir que só temos outliers superiores. Podemos visualizar esses outliers por meio de um boxplot:

sns.boxplot(data=tips, x='total_bill', width=0.2, palette='viridis_r')

7. Correlação entre variáveis

Paramétrica

# Default: .corr(method='pearson')
correlacoes = tips[['tip', 'total_bill']].corr()
correlacoes

	tip	total_bill
tip	1.000000	0.675734
total_bill	0.675734	1.000000

É possível visualizar essas correlção via heatmap:

sns.heatmap(correlacoes, annot=True, cmap='YlGnBu')

Não-paramétrica

# Default: Pearson
correlacoes_spearman = tips[['tip', 'total_bill']].corr(method='spearman')
sns.heatmap(correlacoes_spearman, annot=True, cmap='YlGnBu')

--- title: "Manipulação de Dados com Pandas" author: "Vinícius Oviedo" format: bookup-html+darkonly: embed-fonts: true toc: true --- # Métodos estatísticos Nesta aula, vamos trabalhar com medidas de estatística descritiva em `Pandas`. Aqui, vamos utilizar um conjunto de dados disponível na biblioteca `seaborn`, uma biblioteca de visualização de dados. O conjunto de dados trata de contas e gorgetas em um restaurante fictício. O conteúdo a ser discutido é: 1. Método `describe()` 2. Obtenção de valores máximo e mínimo, além da amplitdue dos dados 3. Medidas de tendência central: média, mediana e moda 4. Medidas de dispersão: desvio padrão, variância, coeficiente de variação 5. Medidas de posição: quartis, percentis, mediana 6. Outliers via método IQR 7. Correlação entre variáveis. Primeiramente, vamos carregar o conjunto de dados `tips`, além das bibliotecas necessárias: ```{python} import pandas as pd import seaborn as sns tips = sns.load_dataset('tips') tips.head() ``` ## 1. Estatísticas descritivas As estatísticas descritivas podem ser obtidas pelo método `.describe()` ```{python} # Vamos mostrar a tabela transposta (T) fins de visualização (linhas viram colunas): tips.describe().T ``` Nesse *dataframe* de saída temos: | Coluna | Descrição | | ------ | --------- | | **COUNT** | Contagem | | **MEAN** | Média | | **STD** | Desvio padrão | | **MIN** | Valor mínimo | | **25%** | Primeiro quartil (`Q1`, 25% dos dados) | | **50%** | Segundo quartil ou **mediana** (`Q2`, 50% dos dados) | | **75%** | Terceiro quartil (`Q3`, 75% dos dados) | | **MAX** | Valor máximo | ### Dica: > Caso queiramos menter dados categóricos também, podemos incluir a opção `include='all'`. ## 2. Mínimo, máximo e amplitude Com essas medidas, podemos responder algumas perguntas. > **Qual foi a gorjeta mínima?** ```{python} tips['tip'].min() ``` > **Qual foi a maior conta (máximo `total_bill`)?** ```{python} tips['total_bill'].max() ``` Logo a amplitude dos dados (para a coluna `tip`) pode ser obtida por: $$ A = Max - Min $$ ```{python} amplitude_gorjetas = tips['tip'].max() - tips['tip'].min() amplitude_gorjetas ``` ## 3. Medidas de tendência central > **Média** ```{python} tips['tip'].mean() ``` > **Mediana** ```{python} tips['total_bill'].mode() ``` > **Moda** ```{python} tips['day'].mode() ``` Conferindo: ```{python} tips['day'].value_counts() ``` ## 4. Medidas de dispersão: > **Desvio Padrão** ```{python} # Amostra (padrão, ddof=1): print(tips['tip'].std()) # População: print(tips['tip'].std(ddof=0)) ``` > **Variância** ```{python} # Amostra (padrão, ddof=1): print(tips['tip'].var()) # População: print(tips['tip'].var(ddof=0)) ``` > **Coeficiente de variação (CV)** ```{python} # Amostra: cv_gorjeta = tips['tip'].std(ddof=1) / tips['tip'].mean() *100 cv_gorjeta = round(cv_gorjeta, 2) print(f' CV para tip: {cv_gorjeta}') ``` ## 5. Medidas de posição: > **Quartis** ```{python} Q1 = tips['tip'].quantile(0.25) Q2 = tips['tip'].quantile(0.5) Q3 = tips['tip'].quantile(0.75) print(f'Q1 (25%): {Q1}') print(f'Q2 (50%): {Q2}') print(f'Q3 (75%): {Q3}') ``` Isso diz muito sobre a distribuição dos dados e pode ser visualizado por um boxplot: ``` sns.boxplot(data=tips, x='tip', width=0.2, palette='viridis_r')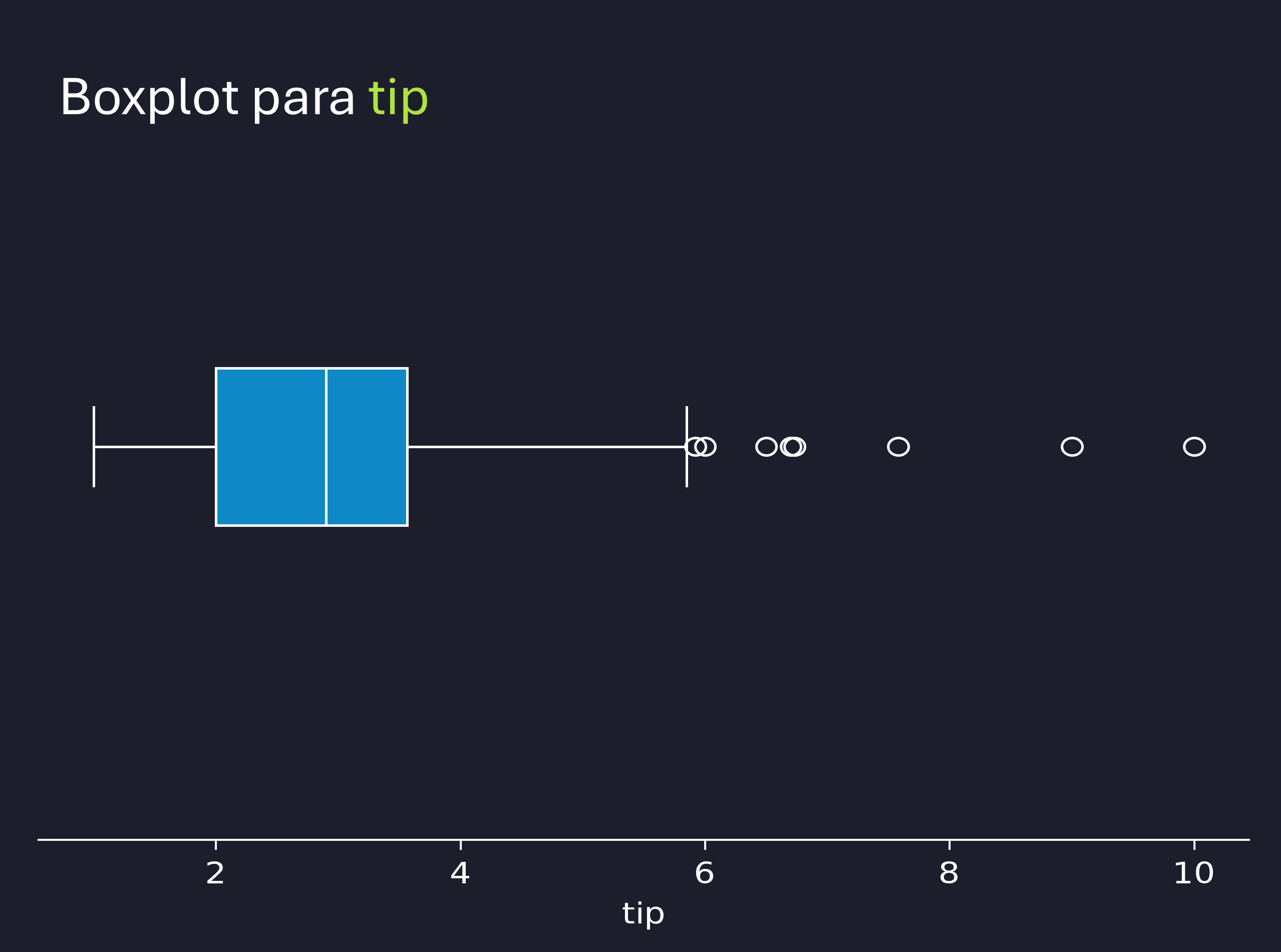 ``` ![Boxplot](assets/boxplot-tip.png){width=450} > **Percentis** ```{python} # Percentil 90°: tips['tip'].quantile(0.9) ``` ## 6. Outliers via método IQR A partir do conhecimento dos quartis e da distância inter-quartil (IQR), dada pela diferença Q3-Q1, podemos encontrar outliers (valores discrepantes): $$ Outliers \ Inferiores = Q_1 - 1.5 IQR $$ $$ Outliers \ Superiores = Q_3 + 1.5 IQR $$ Assim, vamos encontrar outliers para a coluna `total_bill`. ```{python} IQR = tips['total_bill'].quantile(0.75) - tips['total_bill'].quantile(0.25) outliers_inf = tips['total_bill'].quantile(0.25) - 1.5*IQR outliers_sup = tips['total_bill'].quantile(0.75) + 1.5*IQR print(f'Outliers inferiores: {outliers_inf}') print(f'Outliers superiores: {outliers_sup}') ``` Do ponto de vista prático, gorjeta negativa não faz nenhum sentido. Logo, podemos concluir que só temos outliers superiores. Podemos visualizar esses outliers por meio de um boxplot: ```python sns.boxplot(data=tips, x='total_bill', width=0.2, palette='viridis_r')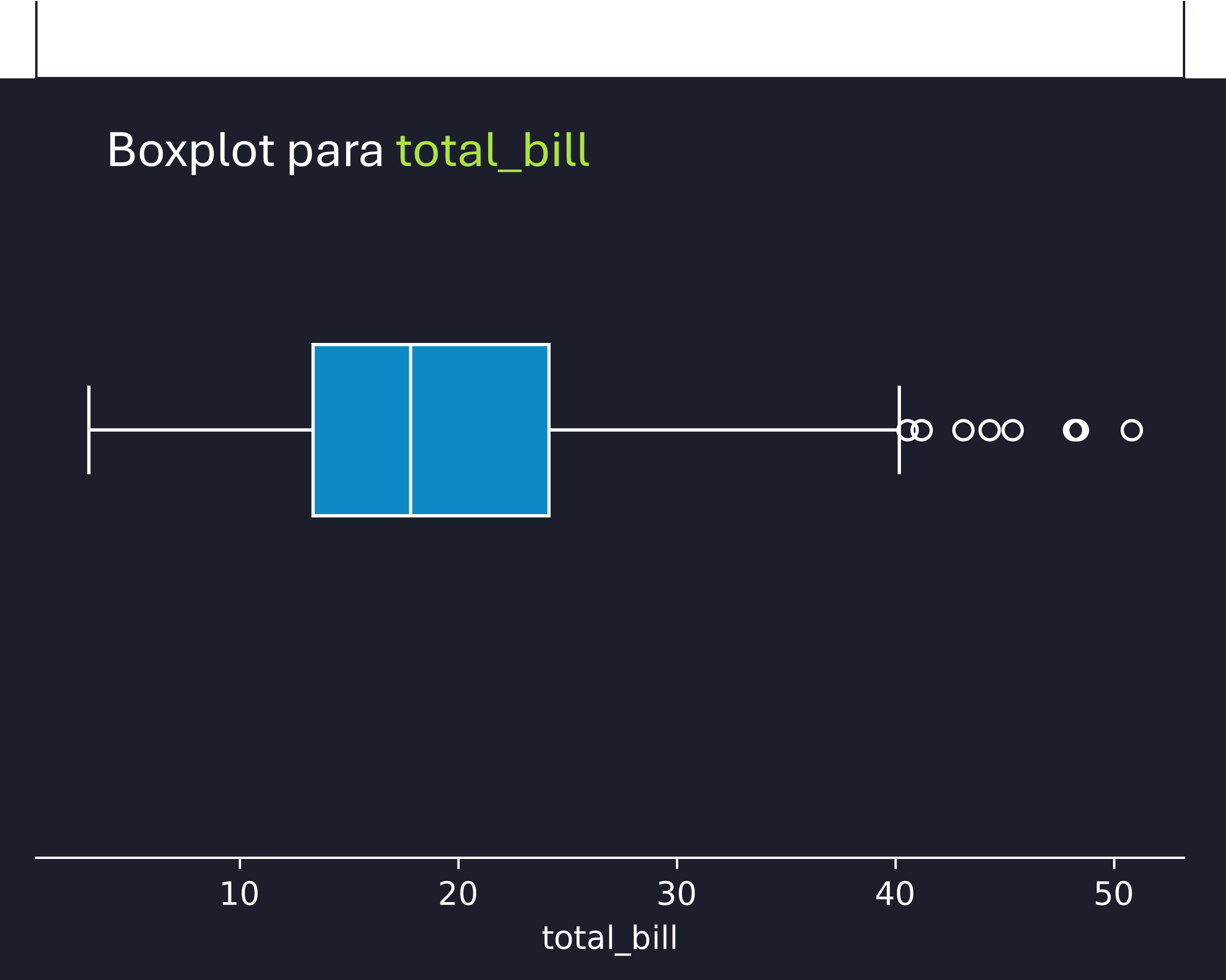 ``` ![Boxplot](assets/boxplot-totalbill.png){width=450} ## 7. Correlação entre variáveis > **Paramétrica** ```{python} # Default: .corr(method='pearson') correlacoes = tips[['tip', 'total_bill']].corr() correlacoes ``` É possível visualizar essas correlção via `heatmap`: ```python sns.heatmap(correlacoes, annot=True, cmap='YlGnBu')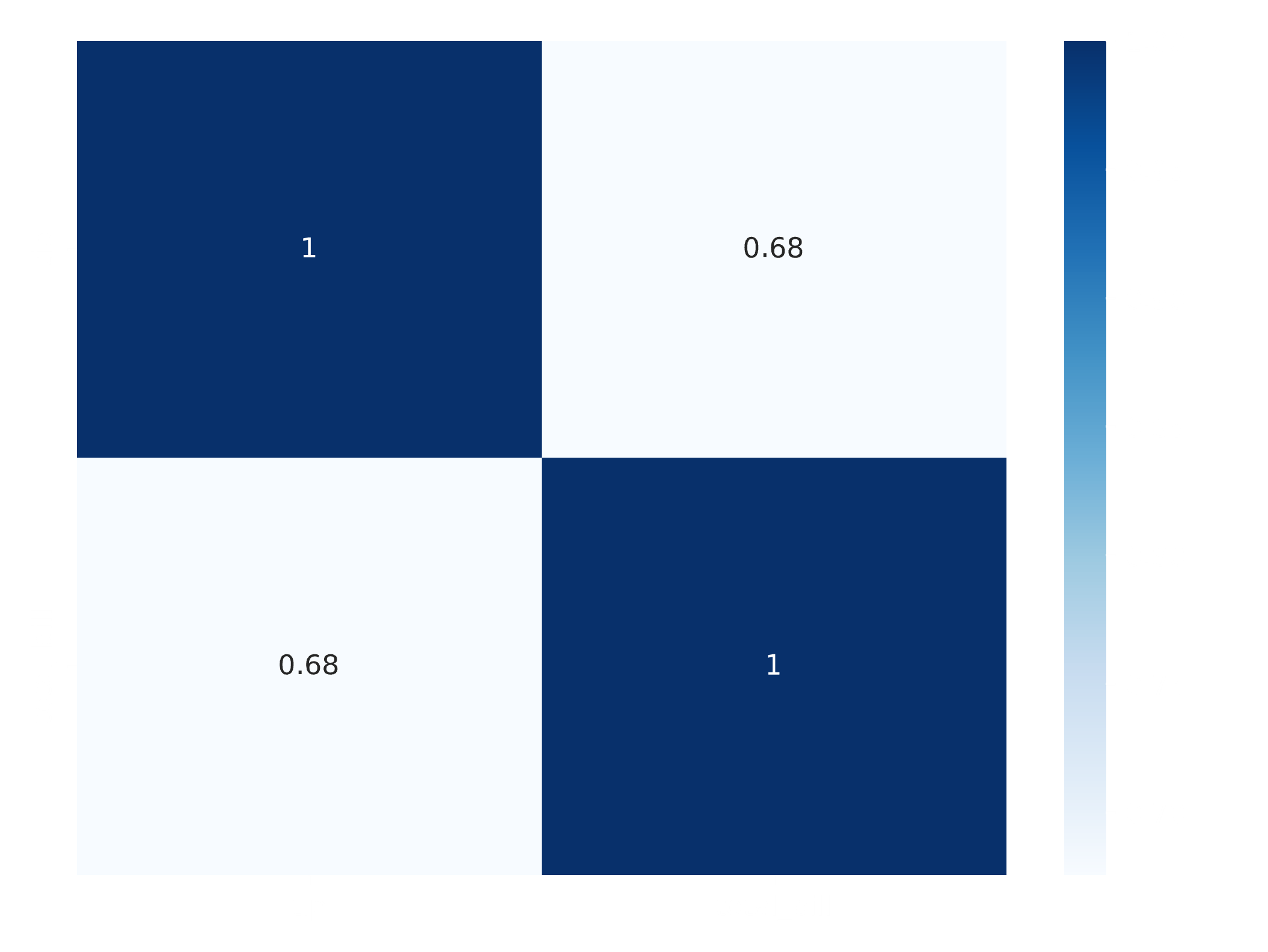 ``` ![Heatmap correlação de Pearson](assets/heatmap-pearson.png){width=520} > **Não-paramétrica** ```python # Default: Pearson correlacoes_spearman = tips[['tip', 'total_bill']].corr(method='spearman') sns.heatmap(correlacoes_spearman, annot=True, cmap='YlGnBu')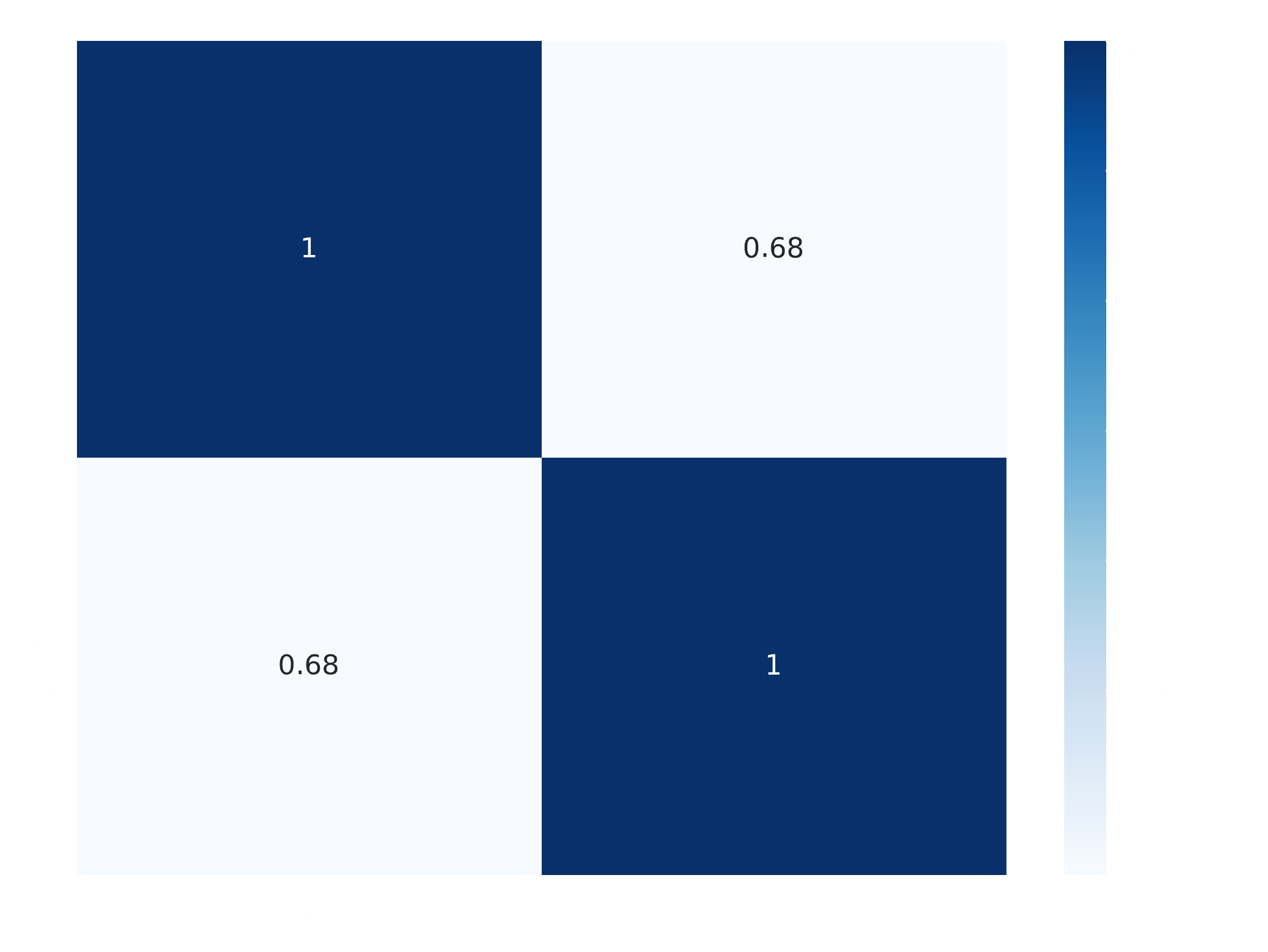 ``` ![Heatmap correlação de Spearman](assets/heatmap-spearman.png){width=520}